MECÂNICA GRACELI GENERALIZADA - QUÃNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [955]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $\psi ^{*}$ [ $\psi ^{*}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS. EM :

O quadripotencial eletromagnético é um quadrivetor definido em unidades SI (e unidades gaussianas em parênteses) como

A^{\alpha }=\left({\frac {\phi }{c}},{\vec {A}}\right)\qquad \left(A^{a}=(\phi ,{\vec {A}})\right)

/ $\psi ^{*}$ [ $\psi ^{*}$

na qual $\phi$ é o potencial elétrico, e ${\vec {A}}$ é o potencial magnético, um vetor potencial.

Os campos elétricos e magnéticos associados com estes quadripotenciais são:

{\vec {E}}=-{\vec {\nabla }}\phi -{\frac {\partial {\vec {A}}}{\partial t}}\qquad \left(-{\vec {\nabla }}\phi -{\frac {1}{c}}{\frac {\partial {\vec {A}}}{\partial t}}\right)

/ $\psi ^{*}$ [ $\psi ^{*}$

{\vec {B}}={\vec {\nabla }}\times {\vec {A}}

/ $\psi ^{*}$ [ $\psi ^{*}$

Ele é útil para agrupar os potenciais nesta forma porque $A_{\alpha }$ $A_{\alpha }$ é um vetor covariante de Lorentz, significando que ele transforma-se do mesmo modo como as coordenadas espaço-tempo (t, x) sob transformações no grupo de Lorentz: rotações e transformação de Lorentz. Como resultado, o produto interno

A^{\alpha }A_{\alpha }=|{\vec {A}}|^{2}-{\frac {\phi ^{2}}{c^{2}}}\qquad \left(A^{a}A_{a}\,=|{\vec {A}}|^{2}-\phi ^{2}\right)

/ $\psi ^{*}$ [ $\psi ^{*}$

é o mesmo em cada quadro referencial inercial.

Frequentemente, físicos empregam a condição gauge de Lorenz $\partial _{\alpha }A^{\alpha }=0$ para simplificar as equações de Maxwell como:

\Box ^{2}A_{\alpha }=-\mu _{0}J_{\alpha }\qquad \left(\Box ^{2}A_{\alpha }=-{\frac {4\pi }{c}}J_{\alpha }\right)

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $J_{\alpha }$ são os componentes do quadricorrente,

\Box ^{2}=\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}

/ $\psi ^{*}$ [ $\psi ^{*}$

é o operador d'Alembertiano.

Em termos dos pontenciais escalar e vetorial, esta última equação torna-se:

\Box ^{2}\phi =-{\frac {\rho }{\epsilon _{0}}}\qquad \left(\Box ^{2}\phi =-4\pi \rho \right)

/ $\psi ^{*}$ [ $\psi ^{*}$

\Box ^{2}{\vec {A}}=-\mu _{0}{\vec {j}}\qquad \left(\Box ^{2}{\vec {A}}=-{\frac {4\pi }{c}}{\vec {j}}\right)

/ $\psi ^{*}$ [ $\psi ^{*}$

Em física de partículas, a teoria de Kaluza-Klein (KK) é uma teoria que visa unificar duas das forças fundamentais da natureza, a gravitação e eletromagnetismo.^[1] A hipótese original foi apresentada por Theodor Kaluza, que remeteu seus resultados a Einstein em 1919,^[2] e a teoria foi publicada pela primeira vez em 1921,^[3] que estendeu a relatividade geral para um espaço-tempo a cinco dimensões.

As equações resultantes podem ser separadas em conjuntos de equações, um desses conjuntos é equivalente as equações de campo de Einstein, outra equivalente as equações de Maxwell para o campo electromagnético e a parte final um campo escalar extra atualmente denominada de "radion" ou "dilaton". Atualmente, sabe-se que essa teoria está sendo usada para a elaboração de uma nova síntese teórica devido à suposição de uma nova partícula no modelo padrão.

Teoria original de Kaluza-Klein[editar | editar código-fonte]

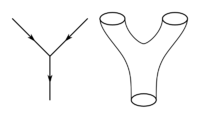
Na teoria de Kaluza –Klein original, para uma entidade geométrica convencional dimensão d estão associados entidades dimensionais d + 1: Um *ponto* espaço-tempo-quadridimensional, portanto, implica numa curva fechada (d = 1), e a trajetória ( d = 1 ) de duas partículas que colidem pode ser pensada e estudada sobre dois tubos unidos (d = 2).

Historicamente, essa abordagem Kaluza-Klein, assim chamada porque as primeiras tentativas nesse sentido foram feitas por Theodor Kaluza (1921) e, um pouco mais tarde, por Oskar Klein (1926), começou como um programa teórico que procurou unificar as forças gravitacional e eletromagnética como efeitos de curvatura de uma variedade pseudoriemanniana em 5 dimensões. Isto é conseguido por equações de Einstein considerando o vácuo em 5 dimensões:

$R_{AB}[g_{AB}]=0$ , com o tensor (em cinco dimensões) Ricci $R_{AB}$ dependendo, o primeiro passo, de uma métrica da forma demonstrada abaixo.

O ponto de partida de Kaluza foi introduzir um espaço-tempo de cinco dimensões no qual o tensor métrico de dito espaço-tempo continha a métrica quadridimensional $g_{ij}\;$ e o potencial vetor $A_{i}\;$ do campo eletromagnético, mais duas funções escalares $\sigma ,\phi$ :

$[{\hat {g}}_{AB}]={\begin{pmatrix}g_{ab}+\kappa ^{2}\phi ^{2}A_{a}A_{b}&\kappa \phi ^{2}A_{a}\\\kappa \phi ^{2}A_{b}&\phi ^{2}\end{pmatrix}}$

Aqui seguimos a convenção de que as maiúsculas latinas A, B,... representam índices tensoriais que vão de 0 a 4, e as minúsculas a, b,... representam índices tensorias de 0 a 3. Assim, as 5 coordenadas de um espaço-tempo de Kaluza seriam $\{x^{A}\}=\{x^{a},x^{4}\}=\{x^{0},x^{1},x^{2},x^{3},x^{4}\}$ , donde a coordenada 0-ésima é a coordenada temporal e a coordenada 4-ésima é a coordenada associada à quinta dimensão adicional e as outras três são as coordenadas espaciais ordinárias.^[4]

O passo seguinte da proposta de Kaluza é impor artificialmente a chamada condição cilíndrica que consiste em impor que nenhuma das componentes do tensor pentadimensional ${\hat {g}}_{AB}\;$ depende da coordenada adicional x⁴, nesse caso, as equações de campo de Einstein^[5] ^[6] se reduzem às condições do eletromagnetismo clássico mais equações da relatividade geral, mais uma equação adicional para o campo escalar adicional:

${\hat {R}}_{AB}-{\cfrac {\hat {R}}{2}}{\hat {g}}_{AB}=0\quad \Rightarrow {\begin{cases}R_{ab}-{\cfrac {R}{2}}g_{ab}={\cfrac {\kappa ^{2}\phi ^{2}}{2}}T_{ab}^{(EM)}-{\cfrac {1}{\phi }}\left[\nabla _{a}(\partial _{b}\phi )-g_{ab}\Box \phi \right]\\\nabla ^{a}F_{ab}=-3{\cfrac {\partial ^{a}\phi }{\phi }}F_{ab}\\\Box \phi ={\cfrac {\kappa ^{2}\phi ^{3}}{4}}F_{ab}F^{ab}\end{cases}}$

$\psi ^{*}$

Estas equações têm a seguinte interpretação: se se considera um espaço-tempo quase-vazio, de topologia ${\mathcal {M}}\times S^{1}$ cinco dimensões com a métrica adequada, então o movimento de uma pequena partícula de prova carregada no mesmo se parece o que teria dita partícula num espaço-tempo de quatro dimensões ${\mathcal {M}}$ no qual se haja introduzido um campo eletromagnético. É dizer, o campo eletromagnético efetivo no qual vê uma partícula carregada no espaço-tempo ordinário pode interpretar-se como o resultado geométrico da curvatura de um espaço-tempo de cinco dimensões.^[7]

Teorias do tipo Kaluza-Klein[editar | editar código-fonte]

As diversas versões das teorias de cordas e supercordas são, de fato, teorias de Kaluza-Klein combinando princípios de quantização. Por exemplo, existem versões de teoria de cordas de 10, 11 e 26 dimensões. Por exemplo, na versão da teoria de supercordas, além da dimensão temporal e das três dimensões espaciais ordinárias, se conjetura que as dimensões adicionais poderiam ter uma topologia de variedade de Calabi-Yau de seis dimensões (isto contrasta com a topologia simples da teoria original de Kaluza na qual a dimensão adicional é um círculo: $S^{1}$ ).

Modernamente, as teorias de Kaluza-Klein também aparecem em cosmologia. Diversos relativistas têm investigado as consequências das equações de Einstein em tempo-espaço de mais de quatro dimensões:

Por exemplo, o enfoque STM ("Space-Time-Matter") é uma teoria em cinco dimensões na qual a dimensão adicional tem a ver com o valor da massa em repouso das partículas. De fato, dentro de certo modelo dentro de dito enfoque a massa de uma partícula variaria segundo a lei:^[8]

${\frac {\dot {m}}{m}}={\frac {A}{t}}$ / $\psi ^{*}$ [ $\psi ^{*}$

$donde:$

m é a massa da partícula,
A uma constante e
t a idade do universo em expansão.

Diversas anomalias detectadas pela Viking quando passava pela órbita de Marte mostraram variações aparentes de ordem $\pm 4\cdot 10^{-12}{\mbox{yr}}^{-1}$ que podem ser explicadas mediante um valor de A = 0,11, dada a idade atual do universo.

Outro enfoque para descrever sua teoria de Expansão cósmica em escala com a ajuda de uma quinta dimensão, tem sido levada em conta o físico C. Johan Masreliez com o que ele chama "Dynamic incremental scale transition", DIST.^[9] Isto conduz a uma possível conexão com a mecânica quântica e um toque de origem da inércia.^[10]

Em mecânica quântica, a equação de Klein–Gordon é a versão relativista da equação de Schrödinger.^[1] Algumas vezes chamada de Klein–Fock–Gordon ou Klein–Gordon–Fock.

É a equação de movimento de um campo escalar ou pseudo-escalar quântico. Este campo descreve partículas sem spin. Esta equação não corresponde a uma densidade de probabilidade definida positiva e além disso é de segunda ordem na derivada temporal, o que impede uma interpretação física simples. Ela descreve uma partícula pontual que se propaga nos dois sentidos temporais e a sua interpretação é possível recorrendo à teoria de antipartículas desenvolvida por Feynman e Stueckelberg. Todas soluções da equação de Dirac são soluções da equação de Klein-Gordon, mas o inverso é falso.

A equação[editar | editar código-fonte]

A equação de Klein–Gordon é derivada aplicando o processo de quantização a relação de energia relativística para uma partícula livre:

$E^{2}=c^{2}{\vec {\textbf {p}}}^{2}+m^{2}c^{4}$

fazendo as identificações padrão ${\vec {\textbf {p}}}\to -i\hbar \nabla$ e $E\to i\hbar \partial _{t}$ , / $\psi ^{*}$ [ $\psi ^{*}$

{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\phi -\nabla ^{2}\phi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\phi =0.

/ $\psi ^{*}$ [ $\psi ^{*}$

que também é frequentemente reescrita de forma mais compacta utilizando o operador d'alembertiano $\Box ={\frac {1}{c^{2}}}\partial _{tt}-\nabla ^{2}$ / $\psi ^{*}$ [ $\psi ^{*}$

$\left(\Box +m^{2}\right)\phi =0$

No contexto de Teoria Quântica de Campos, a equação também pode ser derivada aplicando a equação de Euler-Lagrange para campos:

${\frac {\partial }{\partial x^{\mu }}}\left({\frac {\partial {\mathcal {L}}}{\partial \left(\partial _{\mu }x\right)}}\right)-{\frac {\partial {\mathcal {L}}}{\partial x}}=0$

em que a convenção de soma de Einstein está em uso, à seguinte densidade de lagrangiana:

${\mathcal {L}}={\frac {1}{2}}\left(\partial _{\mu }\phi \partial ^{\mu }\phi -{\frac {m^{2}c^{2}}{\hbar ^{2}}}\phi ^{2}\right)$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Neste contexto, após o processo de segunda quantização, se diz que este campo de Klein-Gordon descreve bósons sem carga, sem spin de massa m.

Versão Complexa[editar | editar código-fonte]

Há uma versão complexa do campo de Klein-Gordon podendo ser derivada da densidade de Lagrangiana:

${\mathcal {L}}={\frac {1}{2}}\left(\partial _{\mu }\phi ^{*}\partial ^{\mu }\phi -{\frac {m^{2}c^{2}}{\hbar ^{2}}}\phi ^{*}\phi \right)$

satisfazendo:

$\left(\Box +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\right)\phi =0~~~~~~~~~~~~\left(\Box +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\right)\phi ^{*}=0$

A este campo $\phi$ estão associados bósons com carga, sem spin de massa m.^[2]

A dinâmica de uma partícula pontual de massa $�$ em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana^[6]^[7]

$L={\frac {1}{2}}m({\dot {q}}^{i})^{2}-V(q)$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

em que $(q^{i},{\dot {q}}^{i})$ (que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e $V(q)$ é o potencial em que a partícula se move. Minimizando o funcional ação

$S=\int dtL(q,{\dot {q}})$

encontra-se a equação de movimento para esse sistema,

$m{\frac {d^{2}q^{i}}{dt^{2}}}=-{\frac {\partial V(q)}{\partial q^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que é a equação de Newton, desde que $\mathbf {F} =-\nabla V(q)$ .

Existe outra formulação equivalente da mecânica clássica, conhecida como formulação hamiltoniana e que pode ser diretamente relacionada a formulação lagrangiana acima. Para se fazer contato entre as duas formulações, define-se o momento

$p^{i}={\frac {\partial L}{\partial {\dot {q}}^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

de maneira que a função hamiltoniana é dada por

$H(q,p)=p^{i}{\dot {q}}^{i}-L(q^{i},{\dot {q}}^{i})$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que para a escolha da lagrangiana acima, tem-se

$H(q,p)={\frac {(p^{i})^{2}}{2m}}+V(q)$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Assim como no caso da função lagrangiana, a hamiltoniana descreve toda a dinâmica de um sistema clássico, portanto, considerando uma variação de $H(q^{i},p^{i})$ tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton

${\dot {q}}^{i}={\frac {\partial H}{\partial p^{i}}},\quad {\dot {p}}^{i}=-{\frac {\partial H}{\partial q^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

e que equivale a equação de Newton, que é de segunda ordem. No formalismo hamiltoniano, usando a regra da cadeia, pode-se escrever qualquer variação temporal de uma função $F=F(t;q(t);{\dot {q}}(t))$ , em termos das equações de Hamilton acima, de modo que,

${\begin{aligned}{\dot {F}}&={\frac {\partial F}{\partial t}}+{\frac {\partial F}{\partial q^{i}}}{\dot {q^{i}}}+{\frac {\partial F}{\partial p^{i}}}{\dot {p^{i}}}\\&={\frac {\partial F}{\partial t}}+{\frac {\partial F}{\partial q^{i}}}{\frac {\partial H}{\partial p^{i}}}-{\frac {\partial F}{\partial p^{i}}}{\frac {\partial H}{\partial q^{i}}}\\&={\frac {\partial F}{\partial t}}+\{H,F\},\end{aligned}}$

onde o parêntese de Poisson é definido como

$\{A,B\}={\frac {\partial A}{\partial p^{i}}}{\frac {\partial B}{\partial q^{i}}}-{\frac {\partial A}{\partial q^{i}}}{\frac {\partial B}{\partial p^{i}}}$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Existem diversas maneiras de realizar a quantização de um sistema clássico, tais como quantização por integrais funcionais e quantização canônica. Esse último método em particular, consiste na substituição do parêntese de Poisson por comutadores^[8]

$\{A,B\}\to {\frac {i}{\hbar }}[{\hat {A}},{\hat {B}}]$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

onde ${\hat {A}},{\hat {B}}$ , são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se

$[{\hat {p}}^{i},{\hat {q}}^{j}]=-i\hbar \delta ^{ij}$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Um aspecto importante a ser observado é que os operadores ${\hat {p}}^{i}$ e ${\hat {E}}$ podem ser representados como os operadores diferencias

${\hat {p}}^{i}=-i\hbar {\frac {\partial }{\partial q^{i}}},\quad ,{\hat {E}}=i\hbar {\frac {\partial }{\partial t}}$

de maneira que a função hamiltoniana, torna-se um operador no espaço de Hilbert, chamado operador hamiltoniano que atua em uma função $\psi (q,t)$

$\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+{\hat {V}}(q)\right)\psi =i\hbar {\frac {\partial \psi }{\partial t}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que é a equação de Schrödinger.

Como foi dito acima, quando Schrödinger primeiro procurou uma equação que regesse os sistemas quânticos, pautou sua busca admitindo uma aproximação relativista, encontrando a depois redescoberta equação de Klein-Gordon:

\left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0

onde

\square \equiv \eta _{\nu \mu }\partial _{\nu }\partial ^{\nu }

A equação de Klein-Gordon, às vezes chamada de equação de Klein-Fock-Gordon (ou ainda Klein-Gordon-Fock) pode ser deduzida de algumas maneiras diferentes.

Usando-se a definição relativística de energia

E^{2}=\left.p^{2}c^{2}+m^{2}c^{4}\right.

chega-se à equação:

{\sqrt {(-i\mathbf {\nabla } )^{2}+m^{2}}}\psi =i{\frac {\partial }{\partial t}}\psi

Essa expressão, por conter operadores diferenciais sob o radical, além de apresentar dificuldades computacionais, também apresenta dificuldades conceituais, já que se torna uma teoria não-local (pelo fato de a raiz poder ser expressa como uma série infinita). Por ser uma equação de segunda ordem não permite que fique bem definida a questão da normalização da função de onda.

Fock deduziu-a através da generalização da equação de Schrödinger para campos magnéticos (onde as forças dependem da velocidade). Fock e Klein usaram ambos o método de Kaluza-Klein para deduzi-la. O motivo, só mais tarde entendido, da inadequação desta equação ao átomo de hidrogênio é que ela se aplica bem somente a partículas sem carga e de spin nulo.

Equação de Dirac[editar | editar código-fonte]

Em 1928 Paul Dirac obteve uma equação relativística baseada em dois princípios básicos

A equação deveria ser linear na derivada temporal;
A equação deveria ser relativisticamente covariante.

A equação obtida por ele tinha a seguinte forma:

i\hbar {\frac {\partial \psi }{\partial t}}={\frac {\hbar c}{i}}\left(\alpha _{0}mc\psi +\alpha _{1}{\frac {\partial \psi }{\partial x^{1}}}+\alpha _{2}{\frac {\partial \psi }{\partial x^{2}}}+\alpha _{3}{\frac {\partial \psi }{\partial x^{3}}}\right)

onde $\alpha _{0}$ , $\alpha _{1}$ , $\alpha _{2}$ e $\alpha _{3}$ não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções $\psi$ são na verdade matrizes coluna da forma

\psi ={\begin{bmatrix}\psi _{1}\\\psi _{2}\\\vdots \\\psi _{N}\end{bmatrix}}

e as matrizes $\alpha _{0}$ , $\alpha _{1}$ , $\alpha _{2}$ e $\alpha _{3}$ devem ser hermitianas.

A equação de Dirac, diferentemente da equação de Klein-Gordon, é uma equação que dá bons resultados para partículas de spin ½. Aliás, um dos sucessos é que esta equação incorpora o spin de forma natural, o que não ocorre com a equação de Schrondinger, onde o spin é admitido posteriormente como uma hipótese ad hoc. Não obstante, isso levou certos autores a afirmarem que o spin é um grau de liberdade relativístico, o que é contestado. Outro sucesso da equação de Dirac foi prever a existência do pósitron, já que a equação previa valores negativos de energia, o que foi inicialmente interpretado, à luz da [[teoria dos buracos], como indicação de elétrons com energias negativas. Essa teoria afirmava que os pósitrons seriam vacâncias produzidas pela promoção desses elétrons para estados com energias positivas. O vácuo é então visto como um mar de elétrons onde eles estariam compactamente colocados. Hoje, entretanto, essa teoria cedeu lugar à questão de criação e aniquilação de partículas num contexto mais geral da quantização canônica dos campos.

Desenvolvimento da teoria quântica dos campos[editar | editar código-fonte]

A origem da teoria quântica dos campos é marcada pelos estudos de Max Born e Pascual Jordan em 1925 sobre o problema da computação da potência irradiada de um átomo em uma transição energética.

Em 1926, Born, Jordan e Werner Heisenberg formularam a teoria quântica do campo eletromagnético desprezando tanto a polarização como a presença de fontes, levando ao que se chama hoje de uma teoria do campo livre. Para tanto, usaram o procedimento da quantização canônica.

Três razões principais motivaram o desenvolvimento da teoria quântica dos campos:

A necessidade da uma teoria que lidasse com a variação do número de partículas;
A necessidade de conciliação entre as duas teorias: mecânica quântica e a relatividade;
A necessidade de lidar com estatísticas de sistemas multipartículas.

Quantização canônica dos campos[editar | editar código-fonte]

Um campo, no esquema conceitual da teoria dos campos, é uma entidade com infinitos graus de liberdade.

O estado de mais baixa energia, chamado de vácuo, corresponde à ausência de partículas.

Estas, entretanto, podem ser criadas ou destruídas através de dois operadores:

$\mathbf {a} _{k}^{+}$ : operador criação
$\mathbf {a} _{k}^{-}$ : operador aniquilação

que agem sobre a função de onda do campo, respectivamente simbolizando a criação e a aniquilação de partículas dotadas de momento $\mathbf {k}$ , possibilidade exigida pela relatividade.

Os operadores, agindo sobre os estados de um tipo específico de espaço de Hilbert, chamado espaço de Fock, criam e destroem as partículas. Entretanto, uma restrição é:

\mathbf {a} _{k}^{-}\left|0\right\rangle =0

o que quer dizer que não pode haver aniquilação sobre o estado básico, já que nesse caso não há partículas a serem aniquiladas.

Pesquisar este blog

MECÂNICA GRACELI GENERALIZADA - QUÃNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [955]

Teoria original de Kaluza-Klein[editar | editar código-fonte]

Teorias do tipo Kaluza-Klein[editar | editar código-fonte]

A equação[editar | editar código-fonte]

Versão Complexa[editar | editar código-fonte]

Equação de Dirac[editar | editar código-fonte]

Desenvolvimento da teoria quântica dos campos[editar | editar código-fonte]

Quantização canônica dos campos[editar | editar código-fonte]

Comentários

Postar um comentário

Postagens mais visitadas deste blog